河 野 二 夫*・ 佐 藤 勝**
*工博 琉球大学教授 工学部土木工学科
**建設省関東地建川治ダム工事事務所
1.緒言
本論文は進行波の中におかれた球形固体粒子が自由落下するときの挙動に関する実験結果と理論的考察の内容を記述したものである.この様な問題は、単に学問的に興味があるというだけでなく、例えば海中物質の浮遊機構の解明とか海洋廃棄物の自由落下処理の問題等に関しても基本的内容を含んでいると思われる.従来この種の研究は多くなされているのであり、例えば平山1)や岩垣・平山2)らは漂砂現象の浮遊機構を解明する目的で進行波や重複波の中の浮遊粒子の挙動について研究を行なっている.球形以外の物体の静水中の落下運動に関しては物体を球形と仮定する時の係数であるshape factorによって抗力係数を評価したAlger & Simonsの研究3)等があり、著者も中空直方体の物体(魚礁構造物)の落下運動について報告した4).従来の研究は漂砂と波との関係、すなわち波による底質の浮遊機構の解明が主な研究目標であったと考えられる.例えば漂砂の鉛直分布特性等に注目した本間・堀川らの研究5)とか野田の研究6)などがあり、他方波の乱れ等に注目した日野7)や堀川ら8)の研究がなされている.本研究は平山らの研究1,2)に類似しているが彼等の場合は球径約2mm程度、沈降速度が約3cm/secであり本論文の場合に対し十分小さい.故に理論的には水平方向および鉛直方向の粒子運動は水粒子速度と球体の沈降速度だけを仮定して解析していると思われる.
本論文では球径がかなり大きいために球体に作用する流体力を仮定し水平および鉛直方向の運動方程式を導き、その近似解と実験結果を比較することによって球体の波による運動(軌跡)を評価しようと試みたものである.
2.実験装置と実験方法
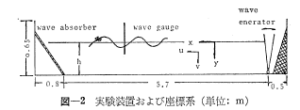
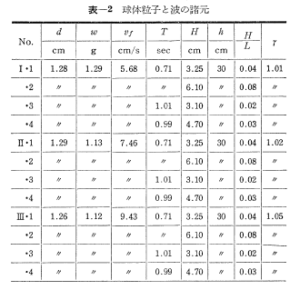
実験は図-2に示すように、琉球大学工学部土木工学科水工実験室に設置してある小型造波水路で水路巾0.4m長さ約6mのものを使用した.水槽の側面はガラス張りであって実験の現象が観測できる様になっている.実験の方法は波を発生させた後5~6波目頃に表-2に示す球体粒子を表面波の峰の位置で落下させストロボを照射して粒子の挙動を撮影し、同時に波高計(容量式)により波形をビジグラフに記録させた.ストロボ照射可能周期は0.75秒~2.26×10-3秒である.粒子の投入位置は水路中央付近で壁面より7cmとし、撮影距離は70cmに固定した.
写真を読み取るため水槽側面に白糸で5cm問隔のメッシュを組み、かつ、ストロボ光のガラス板による反射を防止するためにカメラに偏光フィルターを取りつけた.
実験に使用したストロボ照射周期は0.05秒 と0.10秒である.実験に使用した球体粒子は4種類であるが、比重が1.0の場合の実験結果については本文では省略した.
表-2の記号はd:球の直径、ω:球粒子の重量、γ:比重、vf:静水中の沈降速度、T:波の周期、H:波高、L:波長、h:水路の水深である.
3.理論的考察
図-2に示す様に、粒子投入位置の静水面に座標原点を設け、波の進行方向にx軸、鉛直下向きにy軸を採用する.波動内の任意点の水粒子速度をu、vとし球体粒子の速度と加速度を水平方向と鉛直下向きに対し各々x’、x”;ý、ÿとすればx方向とy方向の球体粒子の運動方程式は次式で与えられる.
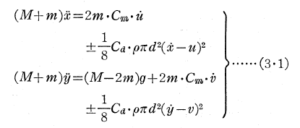
上式でM,mは 各々球体の質量と付加質量;gは重力の加速度、ρは流体の密度;ú、v’は水粒子の水平方向と鉛直下向きの加速度;Cm、Cdは 質量係数と抗力係数である.また右辺の±は相対速度が正の時負の値になる.
一般に、抗力係数はReynolds数により大きく変化するが、質量係数は平均的には1.5程度と見做される9,10)ので本論文ではCm=1.5とする.次に水粒子垂直速度を1周期の中で平均的に見た場合粒子の沈降速度に比較して小さいと仮定しv«ýとする.他方水平方向では水粒子速度が球体の速度に比較して充分大きいと仮定しu»x’とする.
結局、式(3.1)の相対速度に対しては(x’-u)2=u2、(ý-v)2=y2と仮定した.この様な仮定の妥当性については更に検討中であるが近似的には問題はないと考える.さて、微小振幅波理論によよる進行波の波形ηとuは次式で与えられる.
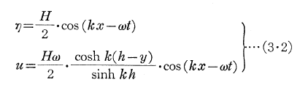
上式でkは波数である.1周期の範囲内での球体の水平方向の移動距離は波長に比較して充分小さいと考えられるので上式で
kx«1として取り扱うならば±u2=±(umax)2・cos2ωtとなる.
故に±は 0<ωt<π/2 および 3π/2<ωt<2πに対し正の値を採用し、π/2<ωt<3π/2の範囲では負の値になる.この条件のもとに±cos2ωtをFourier級数展開すると11)、
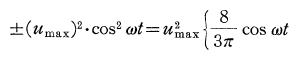
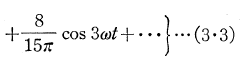
さて、水粒子の速度と加速度の値を式(3・1)に代入し、かつ、以上述べた仮定等を考慮するならば次式が得られる.
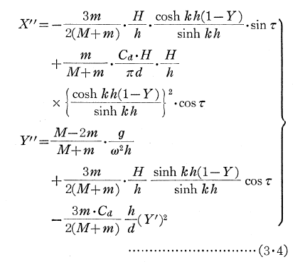
上式はX=x/h、Y=y/h、τ=ωtなる無次元量に関する変換式である.なお、X”=d2X/dτ2、Y”=d2Y/dτ2、
Y’=dY/dτである.t=0 を球粒子の投入時点とするならば、式(3・2)により初期条件と境界条件は次式になる.
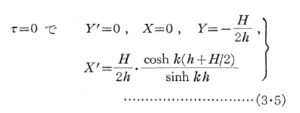
Y”に対する摂動解の第2近似値までの結果は次式になる.
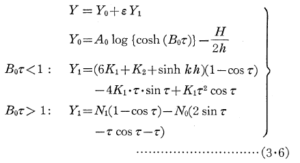
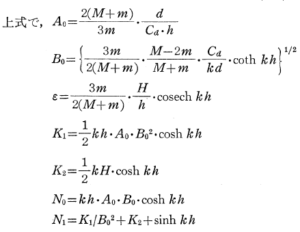
式(3・6)のY0に対する速度はH/2hを無視すると、
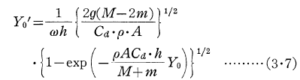
ただし、A=d2π/4である.式(3・7)でhωY’0=ý、hY0=yであるから次式に変換される.
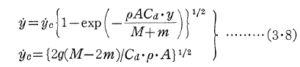
上式は静水中での自由落下速度ýを与えるものであり、ýcは最終速度を示している.故に式(3・6)は球体の自由落下運動(Y0)に波の影響(εY1)が加わった事になる.
次にX方向の運動は式(3・4)の第1式の右辺のYに式(3・6)を代入して積分する事で理解される.Yはτの関数であるので式(3・6)は 極めて複雑な非線型方程式となり解析解を得ることは苦難になる.そこで更に次の仮定を設ける.式(3・4)の第1式の右辺第1項と2項はそれぞれYの点の流体の加速度と速度に関係する項である.従ってYが時間的にどの様に変動したか(Yが時間の関数であること)ではなく、球体の位置(Yの値)がどこにあるのかがX方向の運動に重要な役割をなすと考える.つまりYを各時間に対し固定値として取扱い、その釣合い条件がX方向の運動方程式で与えられると仮定する.(この様な仮定に対し著者自身が十分な確信を得ていないのであるが)積分条件式(3・5)に対する解は次式になる.
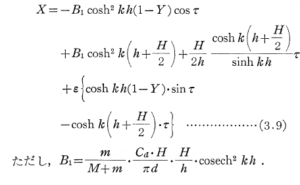
4.実験結果と考察
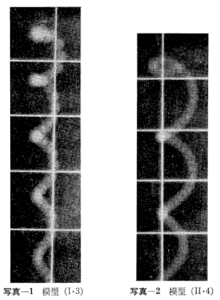
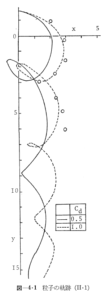
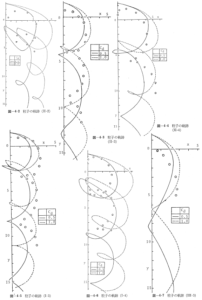
実験で得られたストロボ写真の実例を写真-1~写真-2に示す.次に、式(3・6)によってYの値を計算し、その結果を式(3・9)に代入してXの値を計算した結果が図-4・1~図-4・7に示してある.ただし、球体粒子の座標原点からの位置をcm単位で示したもので、水平方向はx=h・X、鉛直下向きはy=h・Yとして示してある.以上の図から、理論と実験値は一致する傾向にあることがわかる.この様な運動の抗力係数は0.5~1.0の範囲にあることが判断される.また、同一球体粒子の場合は波形勾配が増大する程球体は波の進行方向に落下と共に輸送されることがわかる.
5.結び
比較的球径や沈降速度の大きい粒子が進行波の中におかれて自由落下するときの球体粒子の挙動について実験的、理論的に考察した.理論的には微小振幅波理論から球体粒子に作用する流体力を仮定し、運動方程式を導いて、その近似解を求めた.その結果球体の落下軌跡は理論と実験結果が一致する傾向にある事を示した.なお、抗力係数は0.5~1.0の範囲にある事や波形勾配の増加に伴って球体は落下と共に波の進行方向に輸送されることが判断された.これは球体の沈降作用と波動との相互作用の間に何らかの関係があるものと思われる.この様な実験では理論上の境界条件や初期条件に実験条件が一致しているか否かに問題があると思われる.この理論値の計算は琉球大学電子計算器FACOM-230-15を使用した.関係各位に謝意を表する.
参考文献
1)平山秀夫:進行波における単一粒子の挙動に関する研究、第24回海講論文集、pp.5-9、1977.
2)岩垣雄一・平山秀夫:重複波における浮遊粒子の挙動の特性について、第21回海講論文集、PP.207-213、1974.
3)George、R.A.and D.B.Simons:Fall velocity of irregular shaped particles、Proc.A.S.C.E.、H.D.、pp.721-735、1968.
5)本間仁・堀川清司・鹿島遼一:波による浮遊砂に関する研究、第11回 海講講演集、 pp.159-168、 1964.
6) 野田英明:波による底質の浮遊、第14回海講講演集、pp.306-314.
7) 日野幹雄・大西亮一:浅水表面の粗底上の乱流構造、第18回海講論文集、PP.83-91、1971.
8) 堀川清司・渡辺晃:波運動に伴う乱れと底質の浮遊、第17回海講論文集、 pp.229-233、1970.
9) 河野二夫:球形構造物の波による振動に関する基礎的研究、琉大、理工学部紀要工学篇、No.5、p.147、1972.および同上紀要工学篇、 No.8、pp.37-41、1975.
10) O’Brien、M.D.and J.R.Morison: The forces exerted by waves on objects、 Trans.A.G.U.、Vol.33、No.1、1932.
11) 上記文献9)、 P.140.
原著論文は:河野二夫・佐藤勝;進行波の中の固体粒子の落下運動 第26回海岸工学講演会論文集(1979)pp.668
河 野 二 夫*・ 佐 藤 勝**
*工博 琉球大学教授 工学部土木工学科
**建設省関東地建川治ダム工事事務所